摘要
本文对随机迷宫生成进行了初步的研究和分析，并给出了两种不同的生成算法。最终的算法结合了图的深度优先遍历。通过对比两种算法之间，可发现，在实际问题中，结合了离散数学的方法往往非更有效率且效果更佳。
关键词：随机地图生成(random maze generating)、深度优先遍历(depth-first search)
1. 引言
在平常的游戏中，我们常常会碰到随机生成的地图。这里我们就来看看一个简单的随机迷宫是如何生成。
2. 迷宫描述
随机生成一个m * n的迷宫，可用一个矩阵maze[m][n]来表示，如图：
这里是两个迷宫的例子，其中“[]”表示障碍物(Obstacle block)。以图中第一个迷宫为例，我们可用一个7 * 7的矩阵来表示：
1 1 1 1 1 1 1
0 0 0 0 0 0 1
1 1 1 1 1 0 1
1 0 0 0 1 0 1
1 0 1 1 1 0 1
1 0 0 0 0 0 0
1 1 1 1 1 1 1
( 0 – 可移动；1 – 障碍物 )
3. 迷宫生成算法
随机生成迷宫的方法有很多，这里介绍两种，第一种是作者没有结合离散知识所想出的方法；第二种是作者同学结合了离散数学后所采用的方法。
3.1 一种简单的迷宫生成算法
假定起点在左上角，终点在右下角。方法就是：从起点开始，随机选择一个方向移动，一直移动到终点，则移动的路径便是迷宫的路径。移动过程中要保证路径不要相交，不要超出边界。
下面用图例具体演示一下实现的步骤。以下用Blue Block代表障碍物(obstacle block)，White
Block代表可移动区域(blank block)。先假设整个迷宫都为Blue Block（初始点、结束点除外）。
一、当有多个方向都有可能变为White Block时，需要随机选取一个方向，这就是随机迷宫的来源，如图：
（这时，有下、左、右，三种可选的方向）
二、这里，我们假设随机选了右作为路径的下一步。判断某一方向（黄点）是否可变为White Block，只要这一块都周围有三块为Blue Block就可行，这样就保证了不会出现路径相交的情况，如图：
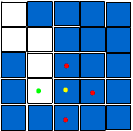（绿点有且仅有一个）
三、如果产生到了一个死胡同（红点），则需回退一格（绿点），再重复上面的步骤，如图。当然，为了实现这要求，需要一个已通过路径的表
（PathList），依次记录所产生的White
Block的坐标，当走入死胡同时，只需pop掉最后一个坐标（设为n），这现在表中最后一个坐标（n-1）即为所需要的。
上面是基本的思路，但有一个问题：如果出现如下情况，如图，则路径表会将所有的元素pop掉，而永远到不了出口。
（永远到不了终点）
解决方案
双路径搜寻，即从入口、出口同时搜寻路径，如图。由于产生那种情况需要White Block越过对角线（如上图，这里是左下角、右上角），所以双路径搜寻可以解决问题（问题没有出现的机会）。
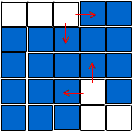
以上是通过很直接的思考方式得来的随机迷宫之实现。
3.2结合图论的迷宫生成算法
3.2.1图的深度优先遍历简介
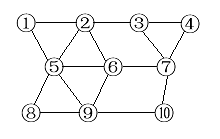
例如，要遍历上面这个图
采取深度优先算法(从1开始)
准备一个Stack s，预定义三种状态：A未被访问 B正准备访问 C已经访问
一、访问1，把它标记为已经访问，然后将于它相邻的并且标记为未被访问的点压入s 中并标记为正准备访问
此时系统状态：
已经被访问的点：1
还没有被访问的点：3 4 6 7 8 9 10
正准备访问的点：2 5 (存放在Stack之中)
二、从Stack中拿出第一个元素 2，标记为已经访问，然后将于它相邻的并且标记为未被访问的点压入s 中并标记为正准备访问，如图：
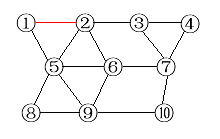
此时系统状态：
已经被访问的点：1 2
还没有被访问的点： 4 6 7 8 9 10
正准备访问的点：3 5 (存放在Stack之中)
三、从Stack中拿出第一个元素 3，标记为已经访问，然后将于它相邻的并且标记为未被访问的点压入s 中并标记为正准备访问，如图：
此时系统状态：
已经被访问的点：1 2 3 4
还没有被访问的点：8 9 10
正准备访问的点：7 6 5 (存放在Stack之中)
依此类推，重复上面的动作，直到Stack为空，即所有的点都被访问。
最后可能的遍历情况，如图：
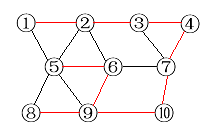
3.2.2深度优先遍历之迷宫生成算法
那么，这样该如何生成迷宫呢？
不知大家注意到了没有，这种算法每一个步骤都要执行一个操作，把刚刚访问过的点的相邻的并且没有标记为被访问过的点压入Stack
s中，然后下一步访问的就是Stack中的第一个元素。那么，当一个点有多个相邻点的话，该按什么顺序压入呢？随机。这就是随机生成迷宫的核心所在！
现在我们换个角度看待问题。
例如需要生成一个5 * 5的迷宫。坐标为(1,1) (3,1) (1,3)
(3,3)的①、②、③、④分别代表节点，它们肯定可让人通过，然后，如果(2,1)设置成可通过，就代表①?②可通过，结合图的遍历算法，我们看到，当
我们从①访问到②时，就把(2,1)设置为可通过，就相当开辟了一条道路，等到遍历结束，迷宫就生成了。
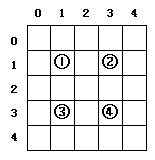
上图中的①②③④，我们可看为一个2 * 2的矩阵，如图：
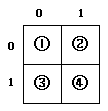
关键是在什么时候“开辟这条道路”。以上节中图的深度优先遍历简介为例子。假设依次访问到的点是：1 2 3 4 7 10 9 8 6 5
当刚刚访问到 9 时，会把8 6 压入Stack中，所以应该开通 9 到 8和6的道路，这样就可自动生成迷宫了。
3.2.3迷宫路径的唯一性
这个算法，大家应该很清楚地看到，从起点到终点的路是唯一的（可以任选两点作为起点和终点）
3.2.4算法的缺点
算法只能生成一个m * n的迷宫，其中m、n都是奇数。
4. 两个算法的对比分析
方法一生成的迷宫：
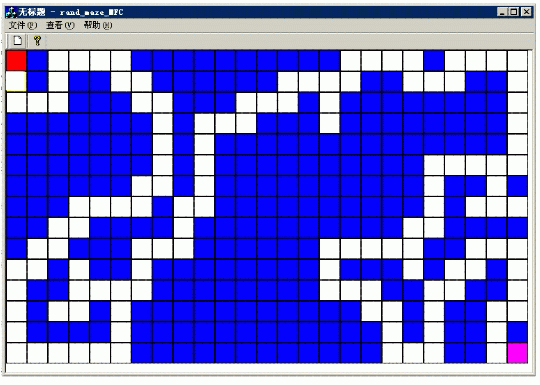
方法二生成的迷宫：
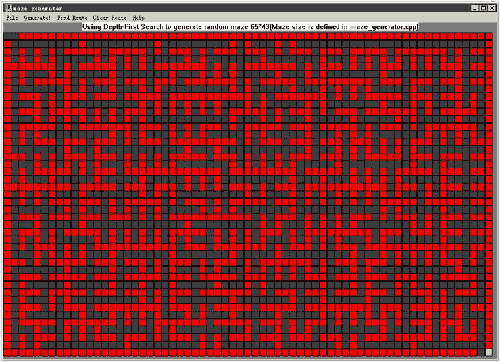
很显然，结合了深度优先遍历(Depth-first search)的算法生成的迷宫要细致许多。
5. 结论
通过对一个简单问题的分析，可以看到，要将离散数学的方法与实际的具体问题相结合，可真正发挥出离散数学的威力。当然，如何将理论与实践相结合，那还需要个人自己去体味。本文仅起抛砖引玉的作用。
参考文献
无